RSA Film-to-cage transformation
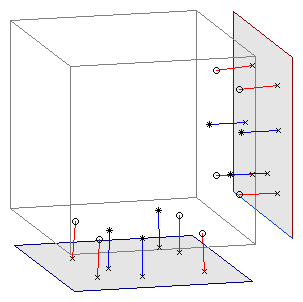
The measured positions of the fiducial markers (the cage markers
closest to the films) are used together with their predefined positions
attached to the cage to calculate a transformation from film
coordinates to cage coordinates. Depending on the assumptions made of
the film position, two different transformation may be calculated.
Parallel (similarity) transformation
If the film can be assumed to be parallel to the fiducial
plane of the cage and the distance between the cage and the film
neglibly small (compared to the distance between the cage and
the X-ray focus), we may use a parallel (similarity) transformation.
The relationship between the measured coordinates 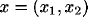 and the corresponding coordinates
and the corresponding coordinates 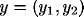 in the fiducial plane may be
described by the following equation:
in the fiducial plane may be
described by the following equation:
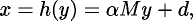
where
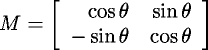
is a rotation matrix, 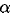 is a
scale factor, and
is a
scale factor, and 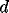 is a
translation vector.
To determine the parameters of this transformation, the following
approximation problem is solved:
is a
translation vector.
To determine the parameters of this transformation, the following
approximation problem is solved:
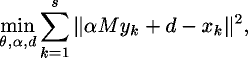
where 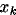 are the measured positions
of the projected fiducial markers
are the measured positions
of the projected fiducial markers 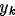 ,
and
,
and  is the number of markers.
There are four unknowns;
is the number of markers.
There are four unknowns; 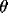 ,
, 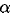 , and the two components of
, and the two components of 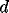 , hence at least two fiducial markers
must be known for the problem to have a unique solution.
, hence at least two fiducial markers
must be known for the problem to have a unique solution.
Projective transformation (central projection)
In the general case when we cannot assume that the film is parallel and/or
close to the cage, the projective transformation, or central
projection, must be used. For the projective transformation, the
relationship between the measured coordinates 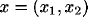 and the corresponding coordinates
and the corresponding coordinates 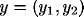 in the fiducial plane may be
described by the following equation:
in the fiducial plane may be
described by the following equation:
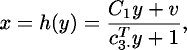
where
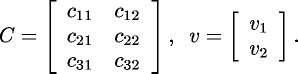
To determine the parameters of this transformation, the following
approximation problem is solved:
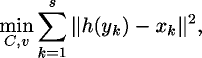
where 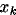 are the measured positions
of the projected fiducial markers
are the measured positions
of the projected fiducial markers 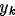 ,
and
,
and  is the number of markers.
There are eight unknowns; the six components of
is the number of markers.
There are eight unknowns; the six components of 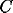 and the two components of
and the two components of 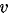 , hence at least four fiducial markers must be known
for the problem to have a unique solution.
, hence at least four fiducial markers must be known
for the problem to have a unique solution.
Performing the film-to-cage transformation
For both transformations, the measured film positions and the known
cage positions of the fiducial markers are used to determine the
parameters of the transformation  . This is illustrated by the red lines in the figure
above.
. This is illustrated by the red lines in the figure
above.
Next, the inverse transformation  is calculated and used to project the positions
of the other markers from the film plane to the cage plane. This is
illustrated by the blue lines in the figure above.
is calculated and used to project the positions
of the other markers from the film plane to the cage plane. This is
illustrated by the blue lines in the figure above.
Last modified: Thu Mar 5 13:58:38 MET 1998


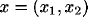 and the corresponding coordinates
and the corresponding coordinates 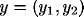 in the fiducial plane may be
described by the following equation:
in the fiducial plane may be
described by the following equation:
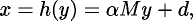
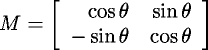
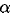 is a
scale factor, and
is a
scale factor, and 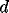 is a
translation vector.
To determine the parameters of this transformation, the following
approximation problem is solved:
is a
translation vector.
To determine the parameters of this transformation, the following
approximation problem is solved:
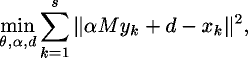
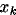 are the measured positions
of the projected fiducial markers
are the measured positions
of the projected fiducial markers 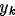 ,
and
,
and  is the number of markers.
There are four unknowns;
is the number of markers.
There are four unknowns; 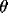 ,
, 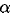 , and the two components of
, and the two components of 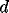 , hence at least two fiducial markers
must be known for the problem to have a unique solution.
, hence at least two fiducial markers
must be known for the problem to have a unique solution.
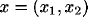 and the corresponding coordinates
and the corresponding coordinates 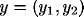 in the fiducial plane may be
described by the following equation:
in the fiducial plane may be
described by the following equation:
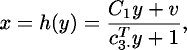

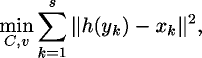
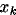 are the measured positions
of the projected fiducial markers
are the measured positions
of the projected fiducial markers 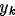 ,
and
,
and  is the number of markers.
There are eight unknowns; the six components of
is the number of markers.
There are eight unknowns; the six components of 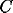 and the two components of
and the two components of 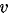 , hence at least four fiducial markers must be known
for the problem to have a unique solution.
, hence at least four fiducial markers must be known
for the problem to have a unique solution.
 . This is illustrated by the red lines in the figure
above.
. This is illustrated by the red lines in the figure
above. is calculated and used to project the positions
of the other markers from the film plane to the cage plane. This is
illustrated by the blue lines in the figure above.
is calculated and used to project the positions
of the other markers from the film plane to the cage plane. This is
illustrated by the blue lines in the figure above.