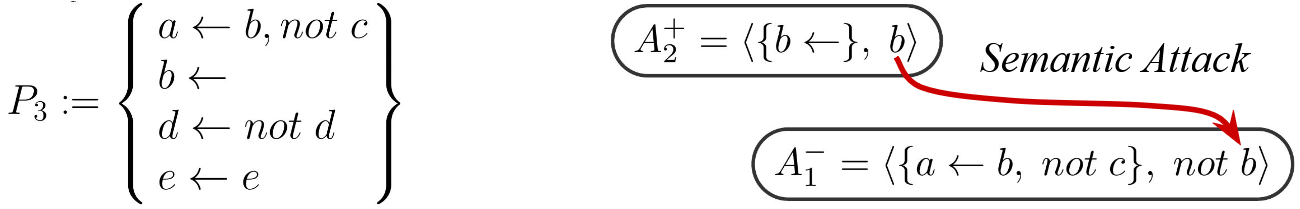Abstract

In this article, we introduce a general framework for structured argumentation providing consistent and well-defined justification for conclusions that can and cannot be inferred and there is certainty about them, which we call semantic and NAF-arguments, respectively. We propose the so-called semantic argumentation guaranteeing well-known principles for quality in structured argumentation, with the ability to generate semantic and NAF-arguments, those where the conclusion atoms are semantically interpreted as true, and those where the conclusion is assumed to be false. This framework is defined on the set of all logic programs in terms of rewriting systems based on a confluent set of transformation rules, the so-called Confluent Logic Programming Systems, making this approach a general framework. We implement our framework named semantic argumentation solver available open source.

Motivation

We propose a general argument construction based on the partial interpretation of programs using different families of logic programming semantics induced by rewriting systems functions [6]. Rewriting rules are used to replace parts of a logic program based on the concept of a normal form, which is the least expression of a program that cannot be rewritten any further [9]. For example, having a program with the only rule: \(innocent(x)\) \(\leftarrow \ not\ guilty(x)\), current structured argumentation approaches [10] generate the only consistent argument: \(\langle \underbrace{\{ innocent(X) \leftarrow \ not \ guilty(x) \}}_{Support}, \ \underbrace{innocent(x)}_{Conclusion} \rangle\), expressing that person \(x\) is innocent if \(x\) can not be proved guilty. However, in domain applications that need the generation of argument-based reason explanations, providing structured and well-defined reasons why \(x\) is not guilty (\(not \ guilty(x)\)) are needed. We emphasize the role of investigating such computational mechanisms that can also build arguments justifying conclusions based on the atoms that are inferred as false, e.g., to state that there is certainty in affirming that the guiltiness of \(x\) is false (there is no evidence), therefore the \(x\) must be innocent, i.e., \(\langle \underbrace{\{ innocent(X) \leftarrow \ not \ guilty(x) \}}_{Support}, \ \underbrace{not \ guilty(x)}_{Conclusion} \rangle\). These types of arguments have been less explored in the formal argumentation theory, except for assumption-based argumentation (ABA) [8].

Syntax and semantics

We use propositional logic with the following connectives \(\wedge,\leftarrow,\;not\), and \(\top\) where \(\wedge\), and \(\leftarrow\) are 2-place connectives, \(\;not\) and \(\top\). The negation symbol not is regarded as the so-called negation as failure (NAF). We follow standard logic programming syntax, e.g., [5], for lack of space we do not include some basic and well-established syntax.

An interpretation of the signature \(\mathcal{L}_P\) is a function from \(\mathcal{L}_P\) to {false,true}. A partial interpretation of \(\mathcal{L}_P\), are the sets \(\langle I_1, I_2\rangle\) where \(I_1 \cup I_2 \subseteq \mathcal{L}_P\). We use \(\texttt{SEM}(P) = \langle P^{true}, P^{false} \rangle\), where \(P^{true} := \{ p |\ p \leftarrow \top \in P\}\) and \(P^{false} := \{ p |\ p \in \mathcal{L}_P \backslash \texttt{HEAD}(P)\}\). \(\texttt{SEM}(P)\) is also called model of \(P\) [6] . We use three value semantics that are characterized by rewriting systems following a set of Basic Transformation Rules for Rewriting Systems (see details in [6]), those rules are named: RED+, RED-, Success, Failure, Loop, SUB, and TAUT. Then, two rewriting systems (\(\mathcal{CS}\)) can be defined based on the previous basic transformations: \(CS_0\) = \(\{RED^+\), \(RED^-\), \(Success\), \(Failure\), \(Loop\) \(\}\), induces the WFS [3]. \(CS_1\) = \(CS_0 \cup \{SUB,TAUT,LC\}\), induces WFS+ [6]. The normal form of a normal logic program \(P\) with respect to a rewriting system \(\mathcal{CS}\) is denoted by \(\mathit{norm}_\mathcal{CS}(P)\). Every rewriting system \(\mathcal{CS}\) induces a 3-valued logic semantics \(\texttt{SEM}_{\mathcal{CS}}\) as \(\texttt{SEM}_{\mathcal{CS}}(P):= \texttt{SEM}(\mathit{norm}_\mathcal{CS}(P))\). To simplify the presentation, we use the entailment \(\models_{\texttt{SEM}_{\mathcal{CS}}}\) applied to a logic program \(P\) is defined by \(\texttt{SEM}_{\mathcal{CS}}(P)=\langle T,F\rangle\) in which \(P \models_{\texttt{SEM}_{\mathcal{CS}}^{T}} a\) if and only if \(a \in T\), similarly, if \(P \models_{\texttt{SEM}_{\mathcal{CS}}^{F}} a\) if and only if \(a \in F\). We use the entailment \(\models_{\texttt{SEM}_{\mathcal{CS}_0}}\) and \(\models_{\texttt{SEM}_{\mathcal{CS}_1}}\) for confluent rewriting system \(CS_0\) and \(CS_1\) respectively; and the form \(\models_{\texttt{SEM}_{\mathcal{CS}}}\) to indicate that any rewriting system can be used.

Semantic and NAF-arguments

Definition 1 (Semantic argument). Given a normal logic program \(P\) and \(S \subseteq P\). \(Arg_P = \langle S, \;g \rangle\) is a semantic argument under \(\texttt{SEM}_{\mathcal{CS}}\) w.r.t. \(P\), if the following conditions hold true:

\(S \models_{\texttt{SEM}_{\mathcal{CS}}^{T}} g\)
\(S\) is minimal w.r.t. the set inclusion satisfying 1.

We simplify the notation of these semantic arguments as \(\mathcal{A}rg^{+}\). Condition 1 states that the interpretation of conclusion \(g\) is true w.r.t. \(T\) in \(\texttt{SEM}_{\mathcal{CS}}(S)\). Condition 2 in Definition 1 guarantees the support minimality.

Definition 2 (NAF-arguments).

Given a normal logic program \(P\) and \(S \subseteq P\). \(Arg_P = \langle S, \; not \;g \rangle\) is a NAF-argument under the \(\texttt{SEM}_{\mathcal{CS}}\) w.r.t. \(P\), if the following conditions hold true:

\(S \models_{\texttt{SEM}_{\mathcal{CS}}^{F}} g\),
\(S\) is minimal w.r.t. the set inclusion satisfying 1.

Condition 1 in Definition 2 is the interpretation of the conclusion w.r.t. \(\models_{\texttt{SEM}_{\mathcal{CS}}^{F}}\), with the set of all the NAF-arguments noted as \(\mathcal{A}rg^{-}\). The addition of \(\; not\) in the conclusion of a NAF-argument stresses that such an atom is interpreted as false by \(\texttt{SEM}_{\mathcal{CS}}\).

Example 1.

Let us consider a program \(P_3\) for building semantic and NAF-arguments considering \(\mathcal{CS}_0\) and \(\mathcal{CS}_1\).

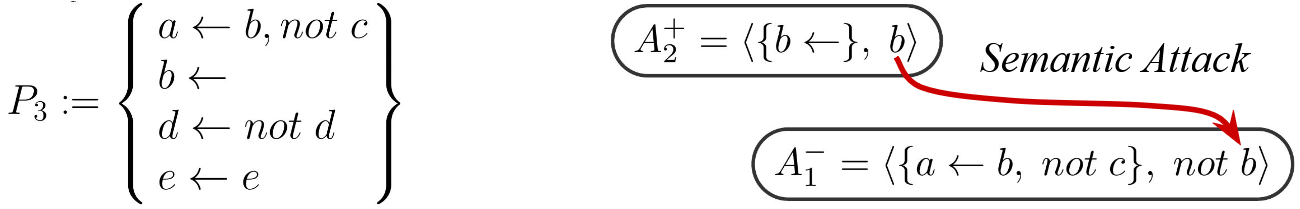
Italian Trulli

We build semantic and NAF-arguments as follows: 1) get related clauses of atoms (\(S_i\)); 2) for every related clause compute \(\texttt{SEM}_{\mathcal{CS}_{0}}(S_i)\) and \(\texttt{SEM}_{\mathcal{CS}_{1}}(S_i)\); 3) the support (every \(S_i\)) is joined to the conclusion¹. Then, the following sets of arguments are built considering \(\mathcal{CS}_0\) and \(\mathcal{CS}_1\):

Case \(\mathcal{CS}_0\): \(\mathcal{A}rg_{P_{3}} = \{A_1^{+},A_2^{+},A_3^{+},A_1^{-},A_2^{-},A_3^{-},A_4^{-},A_6^{-}\}\).

Case \(\mathcal{CS}_1\): \(\mathcal{A}rg_{P_{3}} = \{A_1^{+},A_2^{+},A_3^{+},A_5^{+},A_1^{-},A_2^{-},A_3^{-},A_4^{-},A_6^{-}\}\).

An effect of interpreting argument supports under \(\texttt{SEM}_{\mathcal{CS}}\) is that some atoms (or sets of them) are evaluated in opposition to other arguments (e.g., \(A_1^{+} = \langle S_2,a \rangle\) and \(A_1^{-} = \langle S_1,\; not \; a \rangle\) in Example 1), suggesting a semantic attack relationship.

Definition 3 (Semantic attack). Let \(A = \langle S_A, a\rangle \in \mathcal{A}rg^{+}\), \(B = \langle S_B, not \; b \rangle \in \mathcal{A}rg^{-}\) be two semantic arguments where \(\texttt{SEM}_{\mathcal{CS}}(S_A) = \langle T_A, F_A \rangle\) and \(\texttt{SEM}_{\mathcal{CS}}(S_B ) = \langle T_B, F_B \rangle\). We say that \(A\) attacks \(B\) if \(x \in T_A\) and \(x \in F_B\), denoted \(\texttt{attacks} (x,y)\).

Definition 4 (Semantic Argumentation Framework (SAF)). Let \(P\) be a normal program. Then, a semantic argumentation framework is the tuple: \(SAF_{P}= \langle \mathcal{A}rg_P, \mathcal{A}tt\rangle\)

We can straightforward extend the definitions of argumentation semantics in [7] as follows:

Definition 5. Let \(SAF_{P}= \langle \mathcal{A}rg_P, \mathcal{A}tt\rangle\) be a semantic argumentation framework. An admissible set of arguments \(S \subseteq AR\) is:

stable if and only if \(S\) attacks each argument which does not belong to \(S\).
preferred if and only if \(S\) is a maximal (w.r.t. inclusion) admissible set of \(AF\).
complete if and only if each argument, which is acceptable with respect to \(S\), belongs to \(S\).
grounded if and only if \(S\) is the minimal (w.r.t. inclusion) complete extension of \(AF\)².

Example 2.

Let us consider \(P_5= \{a \leftarrow not \ b; \ b \leftarrow not \ a; \ c \leftarrow not \ c, not \ a; \ d \leftarrow not \ d, not \ b; \}\). \(\texttt{SEM}_{\mathcal{CS}}\) will remove rules involving atoms \(c\) and \(d\). Then, applying Definition 4, we have the framework: \(SAF_{P_5} =\) \(\langle \{A_{6}^{-} = \langle \{a \leftarrow not \ b\}, \; not \ a \rangle\),\(A_{6}^{+} = \langle \{b \leftarrow not \ a\}, \; b \rangle\), \(A_{5}^{-} = \langle \{b \leftarrow not \ a\}, \; not \ b \rangle\), \(A_{5}^{+} = \langle \{a \leftarrow not \ b\}, \; a \rangle \}, \ \texttt{attacks}(A_{5}^{+},A_{6}^{+}),\) \(\texttt{attacks}(A_{5}^{+},A_{6}^{-}),\) \(\texttt{attacks}(A_{6}^{+},A_{5}^{+}),\) \(\texttt{attacks}(A_{6}^{+},A_{5}^{-})\rangle\). When we apply Definition 5 to \(SAF_{P_5}\) we obtained the following extensions:

Stable = preferred: \(\{ \{A_{5}^{+},A_{5}^{-}\}, \ \{A_{6}^{+},A_{6}^{-}\}\}\)
Complete: \(\{ \{A_{5}^{+},A_{5}^{-}\}, \ \{A_{6}^{+},A_{6}^{-}\}, \ \{\}\}\)
Grounded: \(\{ \}\)

Conclusions

The main contributions are: 1) Semantic Argumentation Frameworks (SAF) can be used for justifying true and false interpreted conclusions. 2) SAF is based on families of rewriting confluent systems. 3) Satisfies all the well-known argumentation postulates [1][4]. Future work will involve the exploration of our framework under other Confluent Logic Programming Systems, the satisfaction of other argumentation principles, and the investigation of commonalities between ABA and semantic argumentation.

References

We implemented this procedure and the sources are open, then can be found in https://github.com/esteban-g/semantic_argumentation
In it is shown that grounded can be characterized in terms of complete extensions.