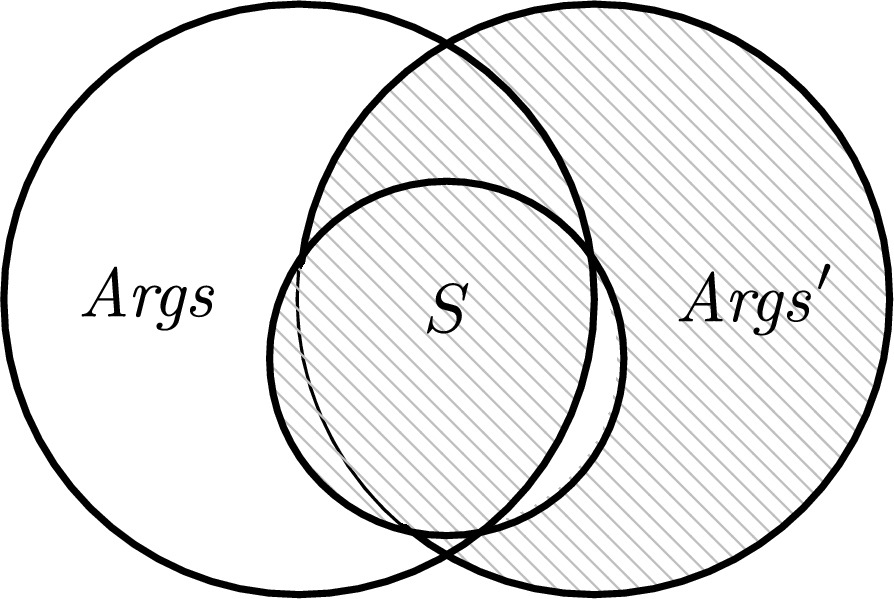Explaining Change in Quantitative
Bipolar Argumentation
Timotheus Kampik1,2, Kristijonas Čyras3, José Ruiz Alarcón1,3
1:Umeå University; 2: SAP Signavio; 3: Ericsson
Recently Published in IJAR...
...And on Github!
#### Motivation: Explaining Change of Inference
* The broader question is fundamental to non-monotonic reasoning.
* We infer $A$ from our knowledge base $\Sigma$.
* After an update of $\Sigma$ to $\Sigma'$, we infer $B \not \supseteq A$.
* What change in our knowledge base explains our change ouf inference?
Kampik & Čyras. *Explanations of Non-monotonic Inference in Admissibility-Based Abstract Argumentation*. 2021.
#### Focus: Quantitative Bipolar Argumentation Frameworks (QBAFs) I
graph TD;
ida(("a (1): 1"))-->|+| idb(("b (1): 2"));
ida-->|-| idc(("c (5): 4"));
linkStyle default stroke-width:3px;
linkStyle 1 stroke-width:3px,stroke-dasharray: 5 5;
#### Focus: QBAFs II
* Interval $\mathbb{I}$, typically real interval, e.g. $\mathbb{I} \in [0, 1]$
* A QBAF is a quadruple
$(Args, \tau, Att, Supp)$ consisting of:
* a set of arguments
$Args$,
* an attack relation
$Att \subseteq Args \times Args$, a support relation
$Supp \subseteq Args \times Args$,
* a total function
$\tau : Args \to \mathbb{I}$
that assigns the initial strength $\tau(x)$ to every $x \in Args$.
Potyka. *Extending Modular Semantics for Bipolar Weighted Argumentation*. 2019.
Baroni, Rago, Toni. *From Fine-Grained Properties to Broad Principles for Gradual Argumentation: A Principled Spectrum*. 2019.
#### Focus: QBAFs III
A **gradual semantics** $\sigma$ defines for $Q = (Args, \tau, Att, Supp)$ a (possibly partial) **strength function** $\sigma_{Q} : Args \to \mathbb{I} \cup \{ \perp \}$ that assigns the **final strength** $\sigma_{Q}(x)$ to each $x \in Args$,
where $\perp$ is a reserved symbol meaning `undefined`.
Potyka. *Extending Modular Semantics for Bipolar Weighted Argumentation*. 2019.
Baroni, Rago, Toni. *From Fine-Grained Properties to Broad Principles for Gradual Argumentation: A Principled Spectrum*. 2019.
#### Focus: QBAFs IV
* There is a considerable research interest in QBAFs,
and even some first hints towards applications.
* QBAFs move argumentation closer to the world of subsymbolic AI.
* Here, we are interested in the **relative change in final strengths of two topic arguments**: Why $b$ and no longer $a$?
Rago et al. *Argumentative Explanations for Interactive Recommendations*. 2021.
Potyka. *Interpreting Neural Networks as Quantitative Argumentation Frameworks*. 2021.
#### Explaining Change in QBAFs
* We want to explain change of inference in QBAFs.
* We have two QBAFs, $Q$ and $Q'$ and two arguments that occur in both $Q$ and $Q'$.
* What is *change*? The arguments change rank (w.r.t. their final strengths) in the order established by the final strength function: the arguments are **strength inconsistent** in $Q$ and $Q'$, given a semantics $\sigma$.
#### Strength (In)consistency I
We say that $a$ is strength inconsistent w.r.t. $b$ iff any of the following does not hold:
* If $\sigma_Q(a) > \sigma_Q(b)$ then $\sigma_{Q'}(a) > \sigma_{Q'}(b)$;
* If $\sigma_Q(a) \< \sigma_Q(b)$ then $\sigma_{Q'}(a) \< \sigma_{Q'}(b)$;
* If $\sigma_Q(a) = \sigma_Q(b)$ then $\sigma_{Q'}(a) = \sigma_{Q'}(b)$.
#### Strength (In)consistency II
What about comparability?
* If two arguments are not comparable in $Q$ but comparable in $Q'$ or vice versa, then we have strength inconsistency.
* We stipulate: arguments with undefined final strengths are not comparable.
#### Example: Strength Inconsistency as Change of Inference
graph TD;
ida(("a (1): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 4")):::topic;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (2): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 0")):::topic;
ide(("e (3): 4"))-->|-|idc;
idd(("d (1): 1"))-->|-|ida
idd-->|+|ide
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1,2,3 stroke-width:3px,stroke-dasharray: 5 5;
#### Explaining Change in QBAFs II
* What are strength inconsistency explanations?
* The arguments:
* that are different between $Q$ and $Q'$ AND
* changes to which are **sufficient** to affect the change of rank
AND (optionally)
* absence of changes to which **counterfactually** mean that the arguments do not change of rank OR
* that collectively meet every sufficient explanation and hence are **necessary** for affecting change of rank.
* We are interested in $\subset$-minimality.
#### Intuition: Sufficient Strength Inconsistency (SSI) Explanations
$\subset$-minimal SSI explanations are
$\\{a\\}$ and $\\{e\\}$.
graph TD;
ida(("a (1): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 4")):::topic;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (2): 2"))-->|+| idb(("b (1): 3")):::topic;
ida-->|-| idc(("c (5): 3")):::topic;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (1): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 1")):::topic;
ide(("e (3): 3"))-->|-|idc;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1,2 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (2): 1")):::exp1-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 0")):::topic;
ide(("e (3): 4")):::exp2-->|-|idc;
idd(("d (1): 1"))-->|-|ida
idd-->|+|ide
classDef topic font-weight:bold
classDef exp1 stroke:red,stroke-width:4px
classDef exp2 stroke:green,stroke-width:4px
linkStyle default stroke-width:3px;
linkStyle 1,2,3 stroke-width:3px,stroke-dasharray: 5 5;
#### Reversal - The Key to Explaining Strength Inconsistency
**Reversal** of $Q'$ to $Q$ w.r.t. $S \subseteq Args \cup Args'$, denoted by $Q_{\leftarrow Q'}(S)$, as a QBAF $(Args^\circ, \tau^\circ, Att^\circ, Supp^\circ)$, where:
* Add S and remove what is in S but not in Args: $Args^\circ = \left( Args' \cup S \right) \setminus (S \setminus Args)$;
* Restore attacks that have originated from S initially and remove the ones that came with the update; clean up 'dangling' attacks: $Att^\circ = (Att'\setminus(S\times Args)) \cup \left(S\times Args^\circ\cap Att \right) \cap (Args^\circ \times Args^\circ)$
* Same for supports: $Supp^\circ = \left(Supp' \setminus(S\times Args)\right) \cup \left(S \times Args^* \cap Supp\right) \cap (Args^\circ \times Args^\circ)$
* Restore the 'initial' initial strengths of arguments in S:
$\tau^\circ: Args^* \rightarrow \mathbb{I}$ and $\forall x \in Args^\circ$ the following statement holds true:
$\tau^\circ(x) = \tau(x), \text{ if } x \in Args \cap S$; $\tau'(x)$, otherwise.
Reversal: Venn
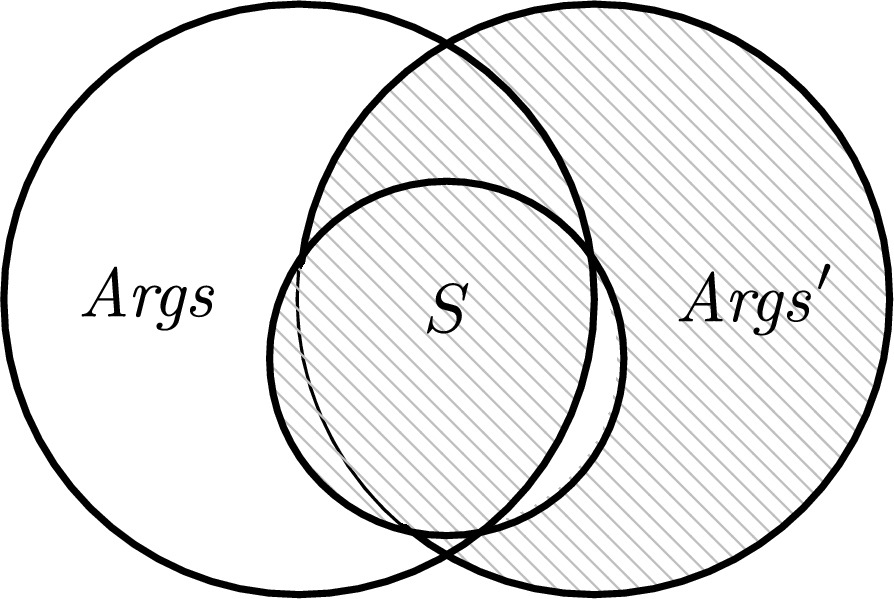#### Reversal: Example
---
title: Q
---
graph TD
ida(("a (1): 1"))-->|+| idb(("b (1): 2")):::topic
ida-->|-| idc(("c (5): 4")):::topic;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1 stroke-width:3px,stroke-dasharray: 5 5;
---
title: Q'
---
graph TD
ida2(("a (2): 1"))-->|+| idb2(("b (1): 2")):::topic;
ida2-->|-| idc2(("c (5): 0")):::topic;
ide2(("e (3): 4"))-->|-|idc2;
idd2(("d (1): 1"))-->|-|ida2
idd2-->|+|ide2
classDef topic font-weight:bold
classDef exp1 stroke:red,stroke-width:4px
classDef exp2 stroke:green,stroke-width:4px
linkStyle default stroke-width:3px;
linkStyle 1,2,3 stroke-width:3px,stroke-dasharray: 5 5;
---
title: "Reversal of Q' to Q w.r.t. {a, e}"
---
graph TD
ida1(("a (1): 0"))-->|+| idb1(("b (1): 1")):::topic;
ida1-->|-| idc1(("c (5): 5")):::topic;
idd1(("d (1): 1"))-->|-|ida1
classDef topic font-weight:bold
classDef exp1 stroke:red,stroke-width:4px
classDef exp2 stroke:green,stroke-width:4px
linkStyle default stroke-width:3px;
linkStyle 1,2 stroke-width:3px,stroke-dasharray: 5 5;
#### Sufficient Strength Inconsistency (SSI) Explanations
$S \subseteq Args' \cup Args$ is an SSI of $a$ and $b$ w.r.t. $\sigma$, $Q$, and $Q'$ iff:
* $a$ is strength consistent w.r.t. $b$ in $Q$, $Q'$ and $S = \emptyset$
* or $a$ is strength inconsistent w.r.t. $b$ in $Q$, $Q'$, as well as w.r.t. $b$ in $Q$, $Q'_{\leftarrow Q(Args \cup Args')\setminus S}$ (when reversing everything but $S$ back).
We are interested in $\subset$-minimal SSI explanations.
#### Once Again: Sufficient Strength Inconsistency (SSI) Explanations
$\subset$-minimal SSI explanations are
$\\{a\\}$ and $\\{e\\}$.
graph TD;
ida(("a (1): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 4")):::topic;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (2): 2"))-->|+| idb(("b (1): 3")):::topic;
ida-->|-| idc(("c (5): 3")):::topic;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (1): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 1")):::topic;
ide(("e (3): 3"))-->|-|idc;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1,2 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (2): 1")):::exp1-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 0")):::topic;
ide(("e (3): 4")):::exp2-->|-|idc;
idd(("d (1): 1"))-->|-|ida
idd-->|+|ide
classDef topic font-weight:bold
classDef exp1 stroke:red,stroke-width:4px
classDef exp2 stroke:green,stroke-width:4px
linkStyle default stroke-width:3px;
linkStyle 1,2,3 stroke-width:3px,stroke-dasharray: 5 5;
#### Counterfactual Strength Inconsistency (CSI) Explanations
$S \subseteq Args' \cup Args$ is a CSI of $a$ and $b$ w.r.t. $\sigma$, $Q$, and $Q'$ iff:
* $S$ is an SSI of $a$ and $b$ w.r.t. $\sigma$, $Q$, and $Q'$
* and $a$ is strength consistent w.r.t. $b$ in $Q$, $Q'_{\leftarrow Q({S})}$ (absent the changes in our explanation).
We are interested in $\subset$-minimal CSI explanations.
#### Example: Counterfactual Strength Inconsistency (CSI) Explanations
The only $\subset$-minimal CSI explanations is
$\\{e\\}$.
graph TD;
ida(("a (1): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 4")):::topic;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (1): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 1")):::topic;
ide(("e (3): 3"))-->|-|idc;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1,2 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (2): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 4")):::topic;
idd(("d (1): 1"))-->|-|ida
classDef topic font-weight:bold
classDef exp1 stroke:red,stroke-width:4px
classDef exp2 stroke:green,stroke-width:4px
linkStyle default stroke-width:3px;
linkStyle 1,2 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (2): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 0")):::topic;
ide(("e (3): 4")):::exp1-->|-|idc;
idd(("d (1): 1"))-->|-|ida
idd-->|+|ide
classDef topic font-weight:bold
classDef exp1 stroke:red,stroke-width:4px
classDef exp2 stroke:green,stroke-width:4px
linkStyle default stroke-width:3px;
linkStyle 1,2,3 stroke-width:3px,stroke-dasharray: 5 5;
#### $\subset$-minimal Necessary Strength Inconsistency (NSI) Explanations
$S \subseteq Args' \cup Args$ is an NSI of $a$ and $b$ w.r.t. $\sigma$, $Q$, and $Q'$ iff
* $S$ is an SSI of $a$ and $b$ w.r.t. $\sigma$, $Q$, and $Q'$
* $S$ meets every SSI explanation.
Here, the notion of necessity only makes sense in case we enforce $\subset$-minimality.
#### Example: Necessary Strength Inconsistency (NSI) Explanations
The only $\subset$-minimal NSI explanation is
$\\{a, e\\}$.
graph TD;
ida(("a (1): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 4")):::topic;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (2): 2"))-->|+| idb(("b (1): 3")):::topic;
ida-->|-| idc(("c (5): 3")):::topic;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (1): 1"))-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 1")):::topic;
ide(("e (3): 3"))-->|-|idc;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 1,2 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
ida(("a (2): 1")):::exp1-->|+| idb(("b (1): 2")):::topic;
ida-->|-| idc(("c (5): 0")):::topic;
ide(("e (3): 4")):::exp1-->|-|idc;
idd(("d (1): 1"))-->|-|ida
idd-->|+|ide
classDef topic font-weight:bold
classDef exp1 stroke:red,stroke-width:4px
classDef exp2 stroke:green,stroke-width:4px
linkStyle default stroke-width:3px;
linkStyle 1,2,3 stroke-width:3px,stroke-dasharray: 5 5;
#### Observation 1: $\subset$-min CSI and NSI explanations are not (always) unique.
$\subset$-minimal CSI and NSI explanations are
$\\{c, d\\}$ and $\\{d, e\\}$.
graph TD;
ida(("a (1): 1"))
idb(("b (6): 6")):::topic;
classDef topic font-weight:bold
graph TD;
ida(("a (1): 5")):::topic
idb(("b (6): 2")):::topic
idc(("c (2): 2")):::exp1-->|+|ida
idd(("d (2): 2")):::exp2-->|+|ida
ide(("e (4): 4")):::exp12-->|-|idb
classDef topic font-weight:bold
classDef exp1 stroke:red,stroke-width:4px
classDef exp2 stroke:green,stroke-width:4px
classDef exp12 fill:green,stroke:red,stroke-width:4px
linkStyle default stroke-width:3px;
linkStyle 2 stroke-width:3px,stroke-dasharray: 5 5;
#### Observation 2: We can handle undefined final strengths...
...but it's a bit weird.
We fix this by defining the class of QBAFs we consider for reversals.
graph TD;
ida(("a (1): 1"))-->|-|idd(("d (1): 0"))
idd-->|-|idb(("b (2): 2")):::topic;
idd-->|-|idc(("c (1): 1")):::topic;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 0,1,2 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
idd(("d (1): ⊥"))-->|-|ida(("a (1): ⊥"))
ida-->|-|idd
idd-->|-|idb(("b (2): ⊥")):::topic;
idd-->|-|idc(("c (1): ⊥")):::topic;
classDef topic font-weight:bold
linkStyle default stroke-width:3px;
linkStyle 0,1,2,3 stroke-width:3px,stroke-dasharray: 5 5;
graph TD;
idd(("d (1): 1")):::exp1-->|-|ida(("a (1): 0"))
idd-->|-|idb(("b (2): 1")):::topic;
idd-->|-|idc(("c (3): 2")):::topic;
classDef topic font-weight:bold
classDef exp1 stroke:red,stroke-width:4px
linkStyle default stroke-width:3px;
linkStyle 0,1,2 stroke-width:3px,stroke-dasharray: 5 5;
#### Basic Analysis (Informal Summary)
Strength inconsistency explanations are sound and complete:
* Without (non-empty) strength inconsistency explanations, no strength inconsistency
* (Non-empty) strength inconsistency explanations imply strength inconsistency
#### Implementation: Scope
* Acyclic QBAFs
* Modular, aggregation-influence semantics that traverse QBAFs starting from unattacked/unsupported nodes
#### Implementation: Analysis
* An NSI explanation is always also an SSI explanation.
* An NSI explanation is a subset of or equal to the union of all $\subset$-minimal SSI explanations.
* For every minimal SSI explanation, an NSI explanation must contain at least one argument of the SSI explanation.
#### Implementation: Sketch
* We make use of the aforementioned properties to reduce our search space.
* We can further exclude arguments that cannot reach the topic arguments in our graph, as well as arguments that have not been changed.
* Finally, we can search through the set of potential explanations by starting with the empty set and then gradually increasing the size of the explanation sets.
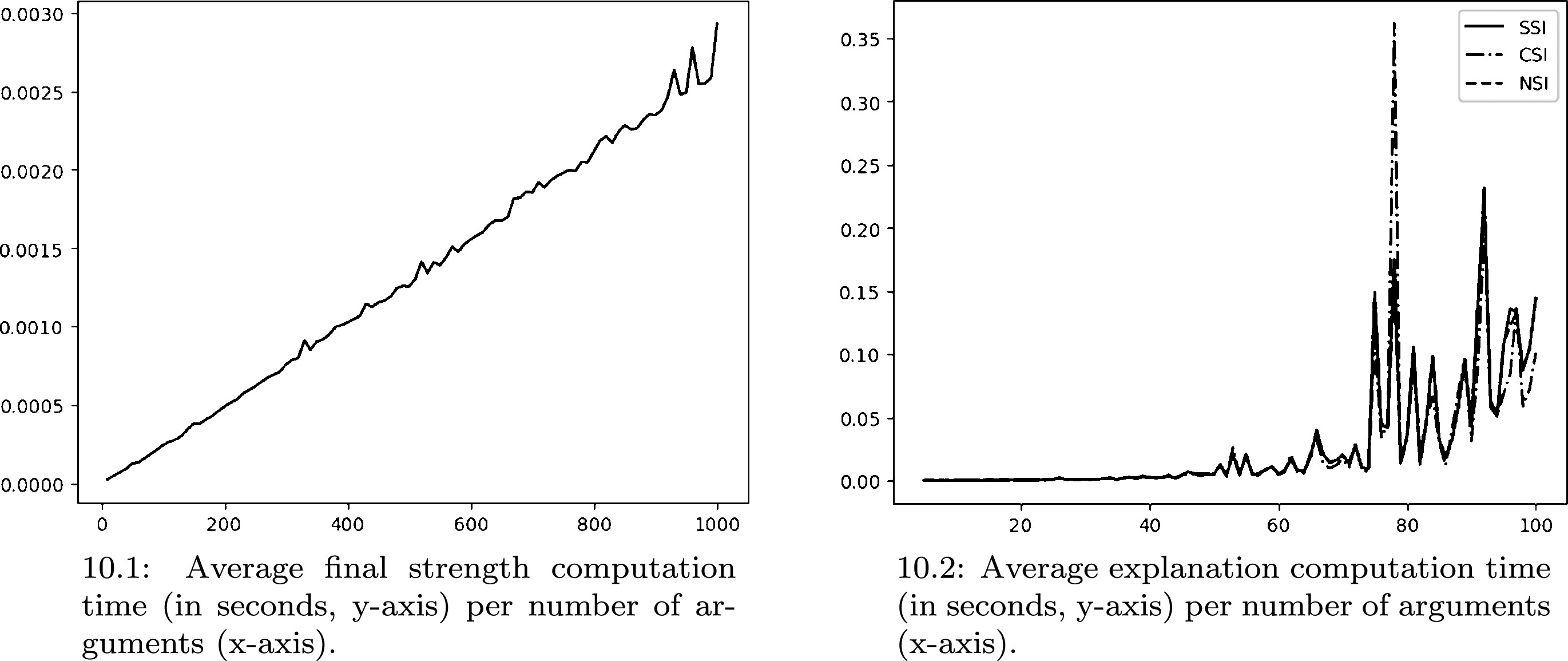
Implementation: Search Example
Implementation: Performance
#### Application to Abstract Argumentation
s: skeptical acceptance; c: credulous acceptance; r: rejection; $s \succ c \succ r$; topic arguments: $a$ and $b$.
graph TD;
ida(("a (⊥): s")):::topic-->|-| idb(("b (⊥): r")):::topic
idb-->|-| ida
idc(("c (⊥): s"))-->|-| idb
classDef topic font-weight:bold
classDef topic font-weight:bold
%%{init: {"flowchart": {"defaultRenderer": "dagre-d3", "padding:2"}} }%%
graph RL;
ida(("a (⊥): r")):::topic-->|-| idb(("b (⊥): s")):::topic
idb-->|-| ida
idc(("c (⊥): r"))-->|-| idb
ide(("e (⊥): s")):::exp1-->|-| ida
idd(("d (⊥): s")):::exp2-->|-| idc
idf(("f (⊥): r"))-->|-| idb
idd-->|-| idf
idc-->|-| idf
classDef topic font-weight:bold
classDef exp1 stroke:red,stroke-width:4px
classDef exp2 stroke:green,stroke-width:4px
#### Future Research
* Generate explanations on edge or 'trace' level
* Extend the implementation (and algorithms) to cover cyclic QBAFs
* Applications!
#### Thank you! Questions?
[Paper link](https://www.sciencedirect.com/science/article/pii/S0888613X23001974)
[Code link](https://github.com/TimKam/Quantitative-Bipolar-Argumentation/)
